Cours de troisième
1 - Puissances et racines carrées
Nous avons déjà vu en quatrième les puissances et les racines carrées.Nous avons vu :
- qu'un nombre n élévé à une puissance p est le résultat du produit de n par n par n par n... p fois (par exemple, 25=2×2×2×2×2=32).
- que la racine carrée d'un nombre n est le nombre positif y tel que y×y=n (par exemple, la racine de 36 est égale 6).
Dans ce cours, nous allons voir comment calculer une puissance lorsque l'exposant est négatif ou nul, et quelques formules qui permettent d'accélérer les calculs dans lesquels apparaissent des puissances et des racines carrées.
As-tu compris les racines carrées ?
Les puissances permettent de manipuler des nombres très grands ou très petits, notamment en astronomie et en chimie en utilisant des écritures scientifiques.
Les racines carrées permettent d'utiliser le théorème de Pythagore et de résoudre deséquations du second degré.
Puissance d'exposant négatif ou nul
Exposant négatif
Nous avons vu la notation an.Si n est positif, on calcule an en calculant a×a×a×...×a : n fois.
Par exemple, 23=2×2×2=8 et (-3)4=(-3)×(-3)×(-3)×(-3)=81 (à ne pas confondre avec -34=-3×3×3×3=-81).
Mais que se passe t-il si n est négatif ?
A quoi est égal 2-3 ?
Pour comprendre les puissances négatives, commence par compléter le tableau ci-dessous.
Conclusion
Pour calculer un nombre avec une puissance négative, on calcule l'inverse de ce nombre avec une puissance positive.
Exemples
As-tu compris ?
Exposant nul
Un nombre élevé à la puissance 0 fait toujours 1, sauf zéro à la puissance zéro qui n'existe pas.Par exemple, 70=1.
Calcul avec des puissances
Rappel
En quatrième, nous avons vu que si x, a et b sont trois nombres, nous avons toujours :Puissance de puissance
Une autre formule utile est la suivante :Puissance d'un produit ou d'un quotient
Voyons enfin deux dernières formules :1.
Calcul avec des racines carrées
Les formules ci-dessous permettent de faire des calculs avec des racines carrées.Formules
1. Si a est un nombre positif, on a toujours :2. On peut vérifier avec une calculatrice que
Si a et b sont deux nombres positifs, on a toujours .
3. Si a et b sont deux nombres positifs (b non nul), on a toujours (en savoir plus, démonstrations).
Addition et soustraction de racines carrées
Attention !On ne peut pas additionner des racines carrées !
Cela reste possible dans certains cas en transformant leurs écritures afin de faire apparaître la racine carrée d'un même nombre.
Exemple
As-tu compris ?
Faux!
On demandait d'écrire avec une seule racine carrée.
Tu as répondu racine de 5.

Essaie encore!
On demandait d'écrire avec une seule racine carrée.
Tu as répondu racine de 5.

Essaie encore!
Simplification de racine carrée
En utilisant les mêmes règles de calcul, voici un exemple un peu plus long.
As-tu compris ?
Remarque
La racine carrée d'un nombre positif, c'est ce nombre à la puissancePar exemple, 640,5=8.
Bravo pour avoir lu ce cours jusqu'au bout.
Maintenant, essaie de faire les exercices !







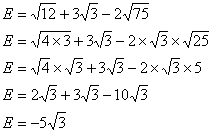

Aucun commentaire:
Enregistrer un commentaire